We’d like to remind Forumites to please avoid political debate on the Forum.
This is to keep it a safe and useful space for MoneySaving discussions. Threads that are – or become – political in nature may be removed in line with the Forum’s rules. Thank you for your understanding.
📨 Have you signed up to the Forum's new Email Digest yet? Get a selection of trending threads sent straight to your inbox daily, weekly or monthly!
Bank miscalculated interest due at end of fixed rate investment - Lessons learnt?
Comments
-
1spiral said:SnowMan said:Economme said:I'm more interested in the general 'lessons learnt', rather than pursuing my own individual case (very low interest! - on many levels)I don't think most systems are set up to provide independent print-offs of how interest has been calculatedBut the info for this must be stored in the systems because most accounts state "interest accrues daily " so it shouldn't be rocket science to add a field to statements that shows these accrued amounts.If you could see how much interest accrues between transactions, it would be quite easy to work out how these figures are arrived at.
You are assuming that the daily interest is calculated daily and then stored against the account. I think this is highly unlikely/ Much more likely that they calculate the total interest when interest payment becomes due.4 -
Clearly I was not looking closely enough at the formula as I didn't notice that caret when I raised the 0.25! The difference will be quite minor when interest is paid monthly, but it will bring in greater error for annual interest. More than the leap year workaround would.TheTelltaleChart said:SnowMan said:The gross interest estimate of £10.28 has been calculated using the formula=IF(G18="Y",I17*(1+H17)^((A18-A17)/365.25)+C18-D18-J18," ")Your use of 365.25 days in a year has already been discussed. The other thing that strikes me is that you're compounding interest daily....Daily compounding is generally going to give less interest than compounding when interest is credited.0 -
TheTelltaleChart said:SnowMan said:The gross interest estimate of £10.28 has been calculated using the formula=IF(G18="Y",I17*(1+H17)^((A18-A17)/365.25)+C18-D18-J18," ")Your use of 365.25 days in a year has already been discussed. The other thing that strikes me is that you're compounding interest daily. That's how I originally assumed it should be done, but when I looked at deposit takers' descriptions of how they calculated interest (which I admit I haven't bothered to do recently), they all seemed to compound only when interest is actually credited.Mathematically: how much interest is accrued overnight, if the starting balance is B, the accrued interest since the last interest payment is A, the interest rate is R%, and there are Y days in a year (e.g. 365.25)?With daily compounding, it's:(B + A) * ( (1 + R/100) ^ (1 / Y) - 1)With compounding when interest is credited, it's:B * R / 100 / Y(Noting that R is not necessarily the same in the 2 formulae: in the first formula, it's the AER, as you specified; in the second, it's the contractual interest rate, which differs from the AER when interest isn't credited annually.)Daily compounding is generally going to give less interest than compounding when interest is credited.The daily compounding I use for simplicity. With daily compounding method you don't need to factor in whether interest is paid monthly, annually or quarterly. But I have added in the compounding when credited calculation into my savings interest spreadsheet as a separate check. And I've made the days in the year used changeable. It requires a separate interest frequency input for the compounding when credited method. I'm tying in actual interest payments exactly to within one pence in most cases using the compounding when credited method. Which is not surprising because as you say it's the method most savings institution use.I agree that the daily compounding method will give less interest than the compounding when credited method on average. But it won't always do. See this example. As an aside note if interest had been payable monthly the annual interest rate column (for the compounding when credited calculation) changes to the gross rate payable monthly i.e. 100 x 12 x (1.05^(1/12) - 1) = 4.889%
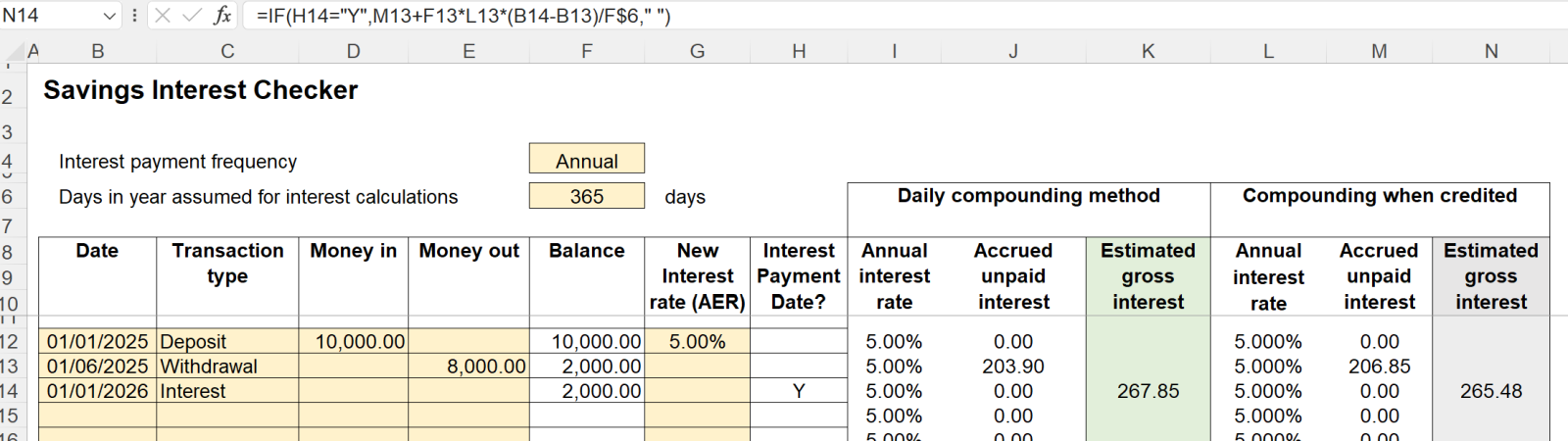 I can make the spreadsheet available if anyone is interested
I can make the spreadsheet available if anyone is interested
I came, I saw, I melted1 -
TheTelltaleChart said:masonic said:
Clearly I was not looking closely enough at the formula as I didn't notice that caret when I raised the 0.25! The difference will be quite minor when interest is paid monthly, but it will bring in greater error for annual interest. More than the leap year workaround would.TheTelltaleChart said:SnowMan said:The gross interest estimate of £10.28 has been calculated using the formula=IF(G18="Y",I17*(1+H17)^((A18-A17)/365.25)+C18-D18-J18," ")Your use of 365.25 days in a year has already been discussed. The other thing that strikes me is that you're compounding interest daily....Daily compounding is generally going to give less interest than compounding when interest is credited.Not necessarily.Surely the error will be least when the actual compounding frequency is greater (it will be completely accurate for the very small number of accounts that do compound daily), a bit less accurate for monthly, and even less accurate for annual. Which was the point I was making.Though if you think the error doesn't increase with decreasing actual compounding frequency (i.e. 365.25 compounding periods is a better proxy for 1 than it is for 12) then that would be interesting to explore in more detail.1 -
Should have said if interest is paid monthly then the two methods will give near identical answers, there isn't long enough between interest payments for the straight line vs curved interest accrual to cause differences, noting that for periods between interest payments where there are no transactions and no interest rate changes the answers are essentially the same. See this example (assumes interest paid away to keep it simple)
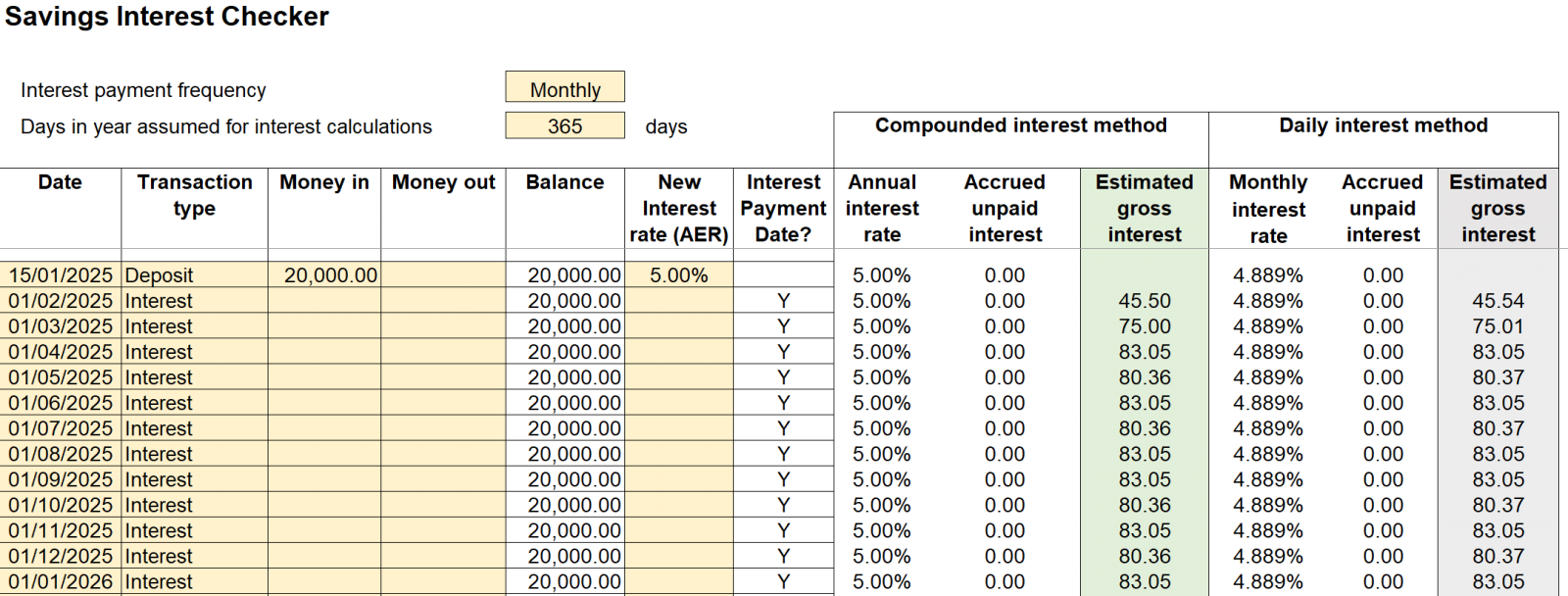 I came, I saw, I melted1
I came, I saw, I melted1 -
TheTelltaleChart said:SnowMan said:I agree that the daily compounding method will give less interest than the compounding when credited method on average. But it won't always do. See this example.Agreed (I got there in a later post).Your example shows daily compounding paying more interest when there is a higher balance earlier in the period, lower later on. If it were the other way round — lower balance earlier, higher balance later — then daily compounding would give less interest. So this part can go either way.Changes in the AER work differently, in that they will always lead to daily compounding paying less interest than compounding when credited.
Another one that causes real differences is if the account pays annual interest and the account is closed after 6 months before the first interest payment, or the first annual interest payment is on a fixed date after 6 months. The compounding when credited works in your favour here.I came, I saw, I melted1 -
TheTelltaleChart said:SnowMan said:The gross interest estimate of £10.28 has been calculated using the formula=IF(G18="Y",I17*(1+H17)^((A18-A17)/365.25)+C18-D18-J18," ")Your use of 365.25 days in a year has already been discussed. The other thing that strikes me is that you're compounding interest daily. That's how I originally assumed it should be done, but when I looked at deposit takers' descriptions of how they calculated interest (which I admit I haven't bothered to do recently), they all seemed to compound only when interest is actually credited.Mathematically: how much interest is accrued overnight, if the starting balance is B, the accrued interest since the last interest payment is A, the interest rate is R%, and there are Y days in a year (e.g. 365.25)?With daily compounding, it's:(B + A) * ( (1 + R/100) ^ (1 / Y) - 1)With compounding when interest is credited, it's:B * R / 100 / Y(Noting that R is not necessarily the same in the 2 formulae: in the first formula, it's the AER, as you specified; in the second, it's the contractual interest rate, which differs from the AER when interest isn't credited annually.)Daily compounding is generally going to give less interest than compounding when interest is credited.To clarify, this is not a daily compound interest formula. A18 and A17 were a month apart. The expression "(1+H17)^((A18-A17)/365.25)" attempts to convert the AER to a gross rate. However, in reality, banks usually set monthly gross rates to a fixed value, regardless of the number of days in the month.It is just a terminology issue, as your illustration below is correct.0
-
Just to put this all into context. This is what the respective interest (paid and accrued but unpaid) looks like using the compounding method used in my checks and the traditional method used by savings institutions, on a lump sum amount saved of £10,000 over 5 years with interest paid annually at a constant 5% AER on the savings anniversary.
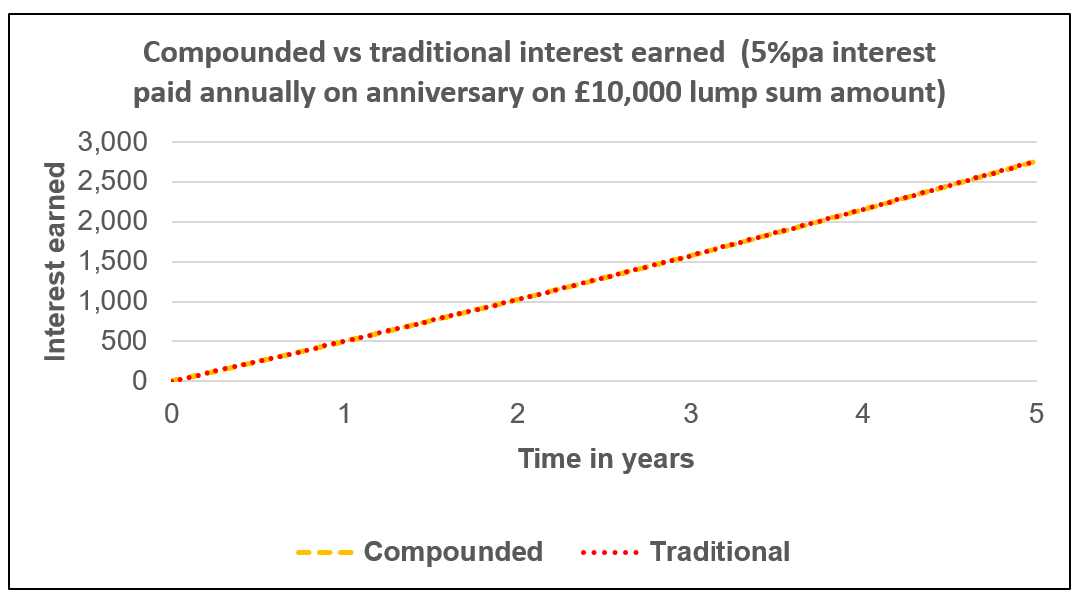 That's why I use the approximation in my spreadsheet. In this case the maximum difference (not visible on the chart because of its small size) is about £3 in interest.Using 365 or 365.25 days has about a 35 pence difference over a year.If we look at what it would look like if the AER was 300% (we wish) over one year this is the result. The same thing is happening in the 5%pa example it's just that the curvature of the compounded line is too small to see in that case
That's why I use the approximation in my spreadsheet. In this case the maximum difference (not visible on the chart because of its small size) is about £3 in interest.Using 365 or 365.25 days has about a 35 pence difference over a year.If we look at what it would look like if the AER was 300% (we wish) over one year this is the result. The same thing is happening in the 5%pa example it's just that the curvature of the compounded line is too small to see in that case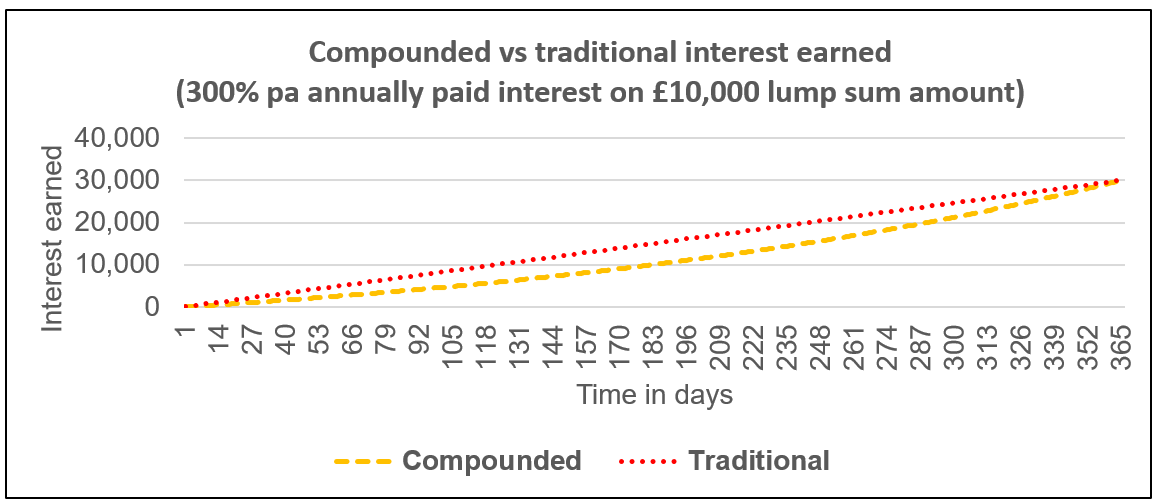 I came, I saw, I melted2
I came, I saw, I melted2
Confirm your email address to Create Threads and Reply

Categories
- All Categories
- 352.5K Banking & Borrowing
- 253.7K Reduce Debt & Boost Income
- 454.5K Spending & Discounts
- 245.5K Work, Benefits & Business
- 601.5K Mortgages, Homes & Bills
- 177.6K Life & Family
- 259.5K Travel & Transport
- 1.5M Hobbies & Leisure
- 16K Discuss & Feedback
- 37.7K Read-Only Boards




