We’d like to remind Forumites to please avoid political debate on the Forum.
This is to keep it a safe and useful space for MoneySaving discussions. Threads that are – or become – political in nature may be removed in line with the Forum’s rules. Thank you for your understanding.
The Top Easy Access Savings Discussion Area
Comments
-
Yes. Using your interpretation I would be interested to know your calculations of the monthly amounts of interest if compounded monthly at gross 1.74% that result in an AER of 1.75%.Mr._H_2 said:
No, you would get interest, calculated on a daily basis. "compounded interest" means "interest paid on interest". Interest cannot compound if it hasn't been added to your account.murphydavid said:
If you closed your account half way into the first month I can assure you you would get compounded interest along with your capital. Its there you just cant see it till the end of the month or on closure.eskbanker said:
No, it's calculated on a daily basis but can't compound until it's actually paid into the account, which is monthly or annually....murphydavid said:
However I can assure you that Shawbrook compounds interest daily its in there T&Cs section 10. There is daily compounding irrespective of how long you keep the account.10.1 Interest is calculated on a daily basis on cleared credit funds and is paid in accordance with the Key Product Information terms.
Let's say you have £1000 in your account and the AER is 2%, paid monthly, and calculated daily.
This would mean that the monthly interest you get paid is "compound interest", because if you leave it in the account, then on the next month, you will get interest on your original amount, plus the interest on the interest.
Your monthly interest rate is therefore 1.02^(1/12) - 1 = 0.16515813%:
So, if you deposit £1000 and leave it in the account for a year, your balance will go like this:balanace at end of month 1 1001.65158 2 1003.30589 3 1004.96293 4 1006.62271 5 1008.28523 6 1009.95049 7 1011.61851 8 1013.28928 9 1014.96281 10 1016.6391 11 1018.31816 12 1020
The daily interest can be calculated from the monthly interest, by dividing the monthly rate by the average number of days in a month:
0.16515813*12/365 = 0.005429856%, which gives 5.43 pence per day in the first month. If you put £1000 in the account, and left it there, the interest calculated for each day of the first month would be 5.43 pence. The calculated amount wouldn't go up until the end of the first month, when instead of calculating the daily interest on £1000, they would calculate the interest on £1001.65.
If the interest compounded daily, the daily rate would be 1.02^(1/365) - 1 = 0.005425525% this is slightly lower than the previously calculated value, due to accounting for the compounding affect which is necessary to end up with the same 2% AER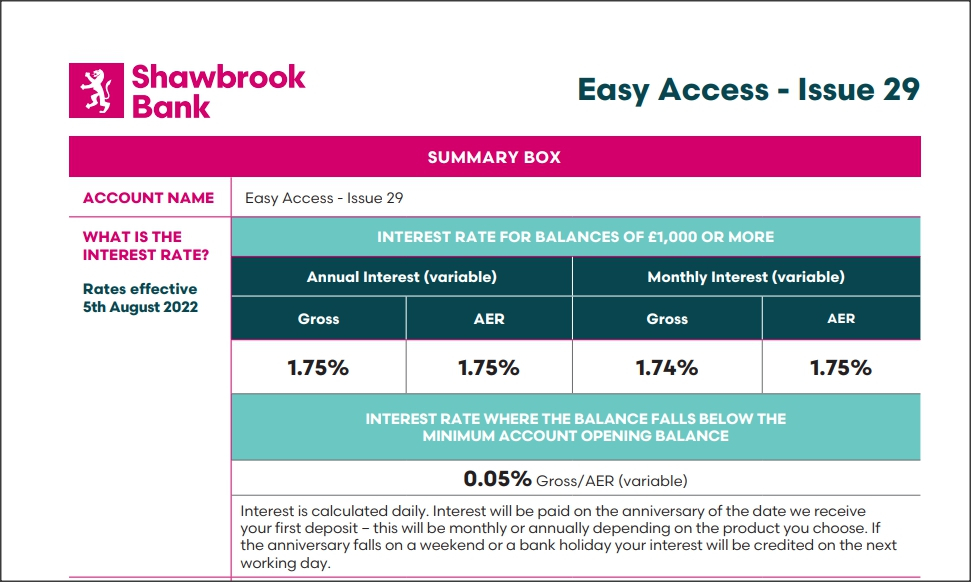
0 -
Coventry 1.55 from 1st Sept1
-
Just noticed their online banking login now has "receive code via SMS" as an option instead of only having the automated call option, which is useful.SJMALBA said:Historic account, not available to new applicants:Coventry Building Society 'Four Access Saver' increasing from 1.5% to 1.85%, effective 1.9.22All other CBS accounts:1 -
Gatehouse Expected Profit rate on their EA ac 1.8% wef 10/08
Easy access account | Gatehouse Bank | Gatehouse Bank plc
0 -
Because of the Gatehouse inclusion later today, 1.55% doesn't make it into the ToTP 10...!Olinda99 said:Coventry 1.55 from 1st Sept
@Coventry_Building_Society Must try harder... 1
1 -
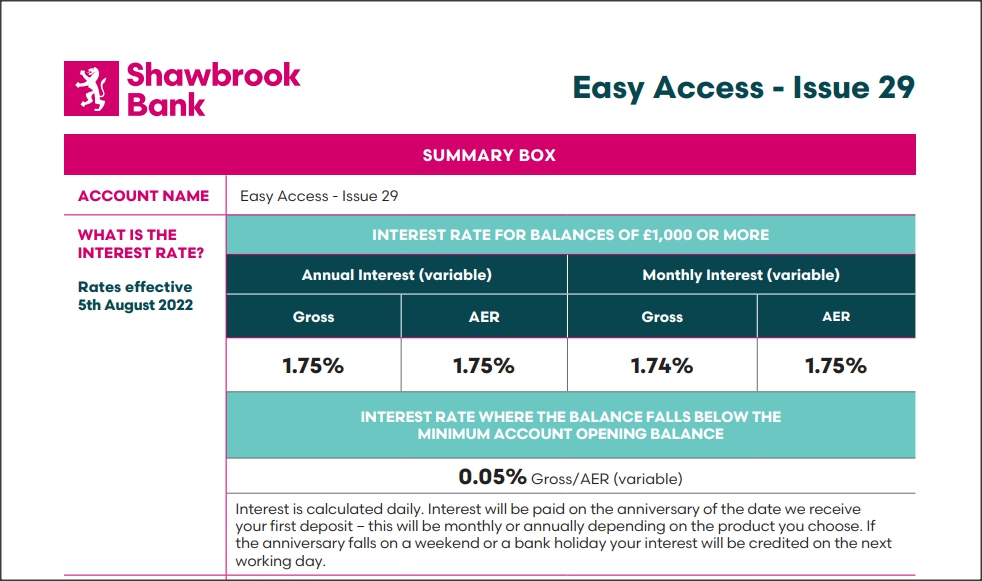
I cant see where you support your claim! So its a bit of a liberty saying I should.eskbanker said:
Closing an account midway through month one makes no difference to the principle - assuming no deposits beyond an opening one, you'd receive interest of (1/365th of the quoted gross rate * number of days * that balance) added to give the final closing balance, but there'd be no compounding involved, as that can only arise when earning interest on interest....murphydavid said:
If you closed your account half way into the first month I can assure you you would get compounded interest along with your capital. Its there you just cant see it till the end of the month or on closure.eskbanker said:
No, it's calculated on a daily basis but can't compound until it's actually paid into the account, which is monthly or annually....murphydavid said:
However I can assure you that Shawbrook compounds interest daily its in there T&Cs section 10. There is daily compounding irrespective of how long you keep the account.10.1 Interest is calculated on a daily basis on cleared credit funds and is paid in accordance with the Key Product Information terms.
If you're asserting that interest is added daily (to allow compounding) then please support that claim with any evidence that contradicts what the Ts & Cs do say.
But I will do my best
Here is the example from Shawbrooks web page
AER Interest: Annual Equivalent Rate Explained | Shawbrook BankExample
If you were to choose a savings account with an interest rate of 5% that paid all interest once at the end of each year, your AER would be 5%:
5% AER = (1 + 0.05/1)^1 − 1
If you invested £500, you would finish the year with £525.
But gross interest rates and AER are only the same if interest is exclusively paid once annually. For example, an account with an interest rate of 2.5% that paid interest twice a year would have an AER of 5.06%:
5.06% AER = (1 + .025/2)^2 − 1
If you invested £500 in that account, you would end the year with £525.30.
You may have assumed the account with a 5% gross interest rate would pay more than the account with 2.5%. But the 2.5% interest rate account will earn more because of compound interest. That’s why it’s essential to use AERs to compare, not gross interest rates.
AER Interest: Annual Equivalent Rate Explained | Shawbrook Bank
Note that the one paying twice a year gives you more cash. In our case they want to pay you the same cash when paying 12 times a year so they show a reduced gross rate.
More important: note that it says "That’s why it’s essential to use AERs to compare, not gross interest rates." So do that. You will see both options have the same AER.
As far as I can see they don't say one way or the other if the daily amount calculated is added on a daily basis so I can't quote that. Can you quote that they don't? But if they did it your way they would have to give you a lump sum at the end of the year to get you to 1.75% AER.
If I'm wrong please explain how using your interpretation can get you to 1.75% at the end of the year.
 0
0 -
murphydavid said: I cant see where you support your claim! So its a bit of a liberty saying I should. <snip>eskbanker said:
Closing an account midway through month one makes no difference to the principle - assuming no deposits beyond an opening one, you'd receive interest of (1/365th of the quoted gross rate * number of days * that balance) added to give the final closing balance, but there'd be no compounding involved, as that can only arise when earning interest on interest....murphydavid said:
If you closed your account half way into the first month I can assure you you would get compounded interest along with your capital. Its there you just cant see it till the end of the month or on closure.eskbanker said:
No, it's calculated on a daily basis but can't compound until it's actually paid into the account, which is monthly or annually....murphydavid said:
However I can assure you that Shawbrook compounds interest daily its in there T&Cs section 10. There is daily compounding irrespective of how long you keep the account.10.1 Interest is calculated on a daily basis on cleared credit funds and is paid in accordance with the Key Product Information terms.
If you're asserting that interest is added daily (to allow compounding) then please support that claim with any evidence that contradicts what the Ts & Cs do say.It's really not difficult. "Monthly interest" is paid monthly. "Annual interest" is paid annually. Interest will be paid to date when either type of account is closed.
Shawbrook show that a Gross Rate of 1.74% paid monthly and allowed to compound will return an Annual Equivalent Rate (AER) of 1.75%.
Your claim: "However I can assure you that Shawbrook compounds interest daily its in there T&Cs section 10. There is daily compounding irrespective of how long you keep the account." is nonsense. You have been invited to fully explain where it was you thought you saw that but have not done so.
You have been given very full and patient explanations, including from Eskbanker. (His username is a clue to why he has so much expertise in banking.) You can contact Shawbrook if you don't accept those explanations.
I think you should now have the good grace to let this drop and apologise.
1 -
The only thing you need to know, in order to determine if the daily interest compounds or not, is: is the interest added to the account daily? As in, can you see it added to the balance of your account every day? If yes, it is compounding daily. If no, it is not compounding daily. The fact that it is not compounding daily does not prevent it from being calculated daily.murphydavid said:
I cant see where you support your claim! So its a bit of a liberty saying I should.eskbanker said:
Closing an account midway through month one makes no difference to the principle - assuming no deposits beyond an opening one, you'd receive interest of (1/365th of the quoted gross rate * number of days * that balance) added to give the final closing balance, but there'd be no compounding involved, as that can only arise when earning interest on interest....murphydavid said:
If you closed your account half way into the first month I can assure you you would get compounded interest along with your capital. Its there you just cant see it till the end of the month or on closure.eskbanker said:
No, it's calculated on a daily basis but can't compound until it's actually paid into the account, which is monthly or annually....murphydavid said:
However I can assure you that Shawbrook compounds interest daily its in there T&Cs section 10. There is daily compounding irrespective of how long you keep the account.10.1 Interest is calculated on a daily basis on cleared credit funds and is paid in accordance with the Key Product Information terms.
If you're asserting that interest is added daily (to allow compounding) then please support that claim with any evidence that contradicts what the Ts & Cs do say.
But I will do my best
Here is the example from Shawbrooks web page
AER Interest: Annual Equivalent Rate Explained | Shawbrook BankExample
If you were to choose a savings account with an interest rate of 5% that paid all interest once at the end of each year, your AER would be 5%:
5% AER = (1 + 0.05/1)^1 − 1
If you invested £500, you would finish the year with £525.
But gross interest rates and AER are only the same if interest is exclusively paid once annually. For example, an account with an interest rate of 2.5% that paid interest twice a year would have an AER of 5.06%:
5.06% AER = (1 + .025/2)^2 − 1
If you invested £500 in that account, you would end the year with £525.30.
You may have assumed the account with a 5% gross interest rate would pay more than the account with 2.5%. But the 2.5% interest rate account will earn more because of compound interest. That’s why it’s essential to use AERs to compare, not gross interest rates.
AER Interest: Annual Equivalent Rate Explained | Shawbrook Bank
Note that the one paying twice a year gives you more cash. In our case they want to pay you the same cash when paying 12 times a year so they show a reduced gross rate.
More important: note that it says "That’s why it’s essential to use AERs to compare, not gross interest rates." So do that. You will see both options have the same AER.
As far as I can see they don't say one way or the other if the daily amount calculated is added on a daily basis so I can't quote that. Can you quote that they don't? But if they did it your way they would have to give you a lump sum at the end of the year to get you to 1.75% AER.
If I'm wrong please explain how using your interpretation can get you to 1.75% at the end of the year.

It is clear that for this product (as with most savings products), Shawbrook start with an AER % that they want to pay, and then back-calculate what the gross rate must be, given the compounding frequency (aka how often is the interest added to the account). For interest added yearly, the gross annual rate will equal the AER. For interest paid monthly, the gross will be ((1+AER)^(1/12)-1)*12. In this case ((1.0175^(1/12))-1)*12 = 1.736119%, which here they have rounded to two decimal places (1.74%).
If the interest compounded daily, the gross rate would be ((1+AER)^(1/365)-1)*365, in this case ((1.0175^(1/365))-1)*365 = 1.734905%, which rounded to two decimal places is 1.73%.0 -
If anyone is interested, Paragon have just increased their Triple Access Cash ISA to 1.55%. Flexible, allows transfers, min £1 and interest is paid monthly or annually.3
-
Trust me it’s easy… I first asked for £10,000 to be transferred from a pittance NatWest interest account and that sailed through.S_uk said:Have opened a Zopa account, easy process and paid in £1 which cleared in about 20 mins. Now for the fun and games transferring larger funds from my Natwest linked account, who were constantly blocking payments I made to Chase.
Did it again for another £10,000 at the end of the day and same…..
I like that you start at the ZOPA account and using Instant Bank Transfer it transfers you to NatWest first. That way you know everything is going to plan.
Yes, it takes around 20 minutes but that has no issues with me.0
Confirm your email address to Create Threads and Reply

Categories
- All Categories
- 352.9K Banking & Borrowing
- 253.9K Reduce Debt & Boost Income
- 454.7K Spending & Discounts
- 246K Work, Benefits & Business
- 602.1K Mortgages, Homes & Bills
- 177.8K Life & Family
- 259.9K Travel & Transport
- 1.5M Hobbies & Leisure
- 16K Discuss & Feedback
- 37.7K Read-Only Boards





