We’d like to remind Forumites to please avoid political debate on the Forum.
This is to keep it a safe and useful space for MoneySaving discussions. Threads that are – or become – political in nature may be removed in line with the Forum’s rules. Thank you for your understanding.
The rule of 70 explained


What Is the Rule of 70?
The Rule of 70 is a simple formula used to estimate the time it takes for an investment to double in size based on its growth rate, taking into account compounding interest over the years. By dividing 70 by the growth rate percentage, you can quickly determine the doubling time.
How Do You Calculate the Rule of 70?
To calculate the Rule of 70, divide 70 by the annual growth rate percentage. For example, if an investment grows at 7% per year, the doubling time is approximately 10 years (70 ÷ 7 = 10).
Why Is the Rule of 70 Useful?
The Rule of 70 provides a quick way to understand the impact of compounding growth rates. It’s commonly used in finance and economics to estimate the doubling time of investments, economies, or populations.
Comments
-
Not something I've encountered before. Seems simple and useful enough.
Have a Thanks 1
1 -
I was taught the 8 and 10 rule. Money at 8% compounded annually would double in 10 years. Money at 10% compounded annually would double in 8 years.
This was based on a savings bonds that were available in my youth. Granted one rarely sees those sort of rates on savings these days.I’m a Forum Ambassador and I support the Forum Team on Debt Free Wannabe, Old Style Money Saving and Pensions boards. If you need any help on these boards, do let me know. Please note that Ambassadors are not moderators. Any posts you spot in breach of the Forum Rules should be reported via the report button, or by emailing forumteam@moneysavingexpert.com. All views are my own and not the official line of MoneySavingExpert.
Click on this link for a Statement of Accounts that can be posted on the DebtFree Wannabe board: https://lemonfool.co.uk/financecalculators/soa.php
Check your state pension on: Check your State Pension forecast - GOV.UK
"Never retract, never explain, never apologise; get things done and let them howl.” Nellie McClung
⭐️🏅😇🏅🏅🏅2 -
My quick calculation suggests that compounding at 8% should double in about 9 years. 1.08^9 = 1.99. And 10% would double in 7.25 years.Brie said:I was taught the 8 and 10 rule. Money at 8% compounded annually would double in 10 years. Money at 10% compounded annually would double in 8 years.
This was based on a savings bonds that were available in my youth. Granted one rarely sees those sort of rates on savings these days.
But as you say, we don't see those kind of rates any more!1 -
For those who are interest in the maths behind the "rule of 70", I've just spent a fun 5 minutes playing around with a graphing calculator.
If you want an exact formula relating the interest rate (x) and the time taken to double (y) you get:
y = log 2 / log (1 + x/100)
A good approximation to this is y = 70 / x (i.e. the rule of 70)
If you plot the two graphs alongside each other, you see how good an approximation it is
(the red line is the "exact" function, the blue line is the "rule of 70")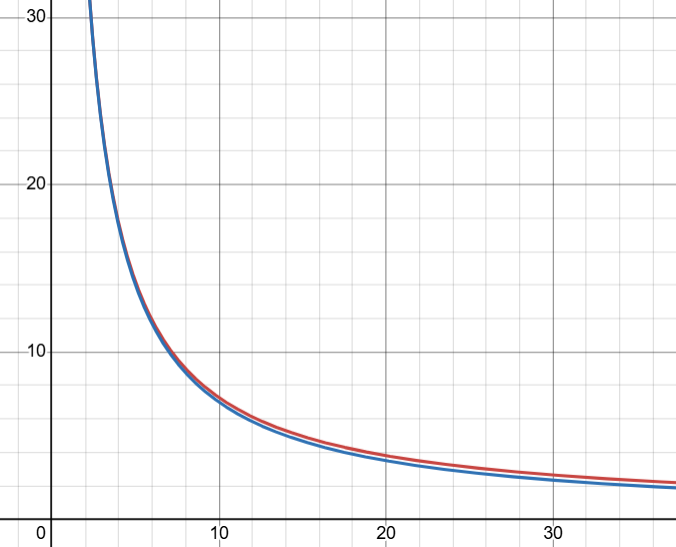
8 -
More like a statement than explanation
 The actual formula for doubling is ln(2)/growth rate, but that can be approximated to 0.69 so using 70/growth% is close enough. Though I like to use 72 just because it has more factors so is easier to do in my head
The actual formula for doubling is ln(2)/growth rate, but that can be approximated to 0.69 so using 70/growth% is close enough. Though I like to use 72 just because it has more factors so is easier to do in my head  3
3 -
Actually 72 looks like a slightly better approximation overall...InvesterJones said:More like a statement than explanation The actual formula for doubling is ln(2)/growth rate, but that can be approximated to 0.69 so using 70/growth% is close enough. Though I like to use 72 just because it has more factors so is easier to do in my head
The actual formula for doubling is ln(2)/growth rate, but that can be approximated to 0.69 so using 70/growth% is close enough. Though I like to use 72 just because it has more factors so is easier to do in my head 
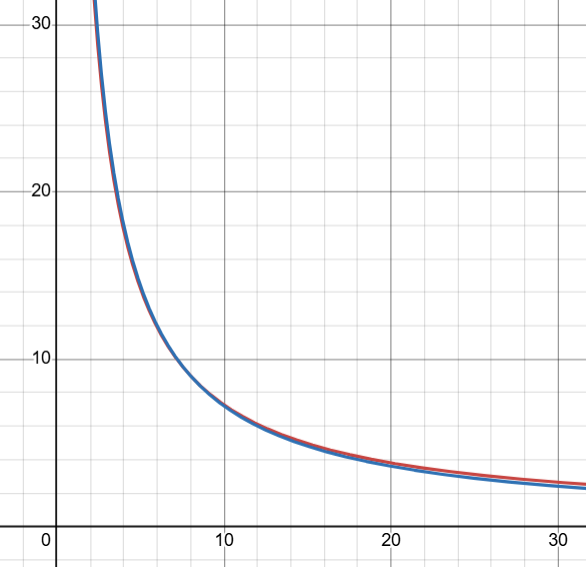
Although for rates of around 5% then 70 is more accurate than 72
71 is even more accurate!1 -
Still quite useful for investment returns.clairec666 said:
My quick calculation suggests that compounding at 8% should double in about 9 years. 1.08^9 = 1.99. And 10% would double in 7.25 years.Brie said:I was taught the 8 and 10 rule. Money at 8% compounded annually would double in 10 years. Money at 10% compounded annually would double in 8 years.
This was based on a savings bonds that were available in my youth. Granted one rarely sees those sort of rates on savings these days.
But as you say, we don't see those kind of rates any more!1 -
The rule of 70 is pretty accurate, and it gets more accurate with lower interest rates. For instance, 1% doubles in 69.661 years, because 1.01 to the power of 69.661 is 2. 2% doubles in 35.003 years. 3% doubles in 23.45 years (23.45*3=70.35), etc.
I think the true number to use with very low interest rates and long periods is rather than "70" is 100 times the natural log of 2, which is 69.315, but "70" is obviously easier to work with (and almost exactly right for 2%, anyway). As the interest rate gets smaller and smaller, the product of the rate and the years gets closer and closer to that. And it works with other ratios - eg to triple your money it would be a rule of 100*ln(3)=110, more or less.
I think once upon a time I could have proved this, but not now.
1 -
interesting post, I envy you all, as you seem to understand this and have a discussion..Would anyone mind sharing how do you get to know what you know about the calculations? is it from being taught and/ or keep reading and learning? I ask as I would like to be able to follow posts, usually they may seem basic to most but I find it quiet advance (one example is 'EthicsGradient' reply even though gave a breakdown of their calculations, I am still not always understand and do not know what to look up to teach myself, as it will be helpful for me to do my financial planning etc. thanks
1 -
20122013 said:Would anyone mind sharing how do you get to know what you know about the calculations?For me it was nothing to do with financial matters, I first learned about it at school in physics and chemistry: https://en.m.wikipedia.org/wiki/Half-lifeObviously here we are running it backwards to get a doubling time but the principles are the same.1
Confirm your email address to Create Threads and Reply

Categories
- All Categories
- 353.8K Banking & Borrowing
- 254.2K Reduce Debt & Boost Income
- 455.2K Spending & Discounts
- 246.8K Work, Benefits & Business
- 603.3K Mortgages, Homes & Bills
- 178.2K Life & Family
- 260.9K Travel & Transport
- 1.5M Hobbies & Leisure
- 16K Discuss & Feedback
- 37.7K Read-Only Boards





