Hargreaves Lansdown and Interactive Investor unlock new gilt issues for DIY investors

gm0

No problem.  Happy to clarify what I thought needed to be more explicit.  Clarification not contradiction.  Hopefully we don't disagree about how bonds work.

The original entire text that I replied to:

>No, you do not get your original investment back on maturity. The maturity value could be more or less than what >you paid, and is very unlikely to be equal to what you paid. If interest rates fall more than the market expects, the >current market price will rise

The bit that confuses (in my opinion) is the combination of the last two sentences. As they seem to imply what you get is market value and that market value is a variable with interest rates.  It does not talk about redemption of principal being a fixed quantity. Hence the space for misinterpretation.

I read the above paragraph in toto as communicating the idea that "current market price" at the end is a variable. And that a current market price not nominal value is what you actually get.  So the end value is thus a variable due to interest rates changing.  I am asserting the idea that at redemption the nominal (or indexed for linkers) principal is what you get.  So this is a known fact.  The fixed redemption value of the bond and not a resale value from the journey.  As the bond passes last coupon and approaches expiry the difference between these two erodes. So this may seem picky.

But the point I am making is that redemption of principal after coupons is a locked in cashflow - purchased for a known price (which may indeed be different to the nominal principal) at the start or later via resale market of older bonds.

Central bank interest rates from the date of purchase onward are irrelevant *if* the bond is to be held to maturity to term. 

As introduced above - bond funds with a maintained average duration and constant resale and repurchase to achieve that are locking in market prices along the interest rate journey - and so work in the other way - and so ARE sensitive to central bank interest rate changes.  As everybody just found out again in the 100 year rapid interest rate rises event.  This difference is one of the least intuitive things about the bond market for novice retail investors not working in the trade. At the risk of generalising from self and my own conceptual struggle with it. 

I am NOT claiming the other poster doesn't know this or is wrong in the sentences individually. 
I am suggesting we can explain better to OP their question about maturity value.

What you pay upfront - for a locked in cashflow - coupon coupon coupon returned principal - is indeed a variable.
As is the possible resale value going up and down during the journey. 
We all agree purchase price is a variable.  And method dependent. 

This is fixed by the purchase transaction at auction or other market mechanism. So known once done. You are done if holding to term.  Paid the variable price a point in time to lock in fixed cashflow.  Hence self-annuitisation, bond ladders etc. Purpose dependent.

And we agree that value along the way for resale is variable (with central bank rates changing causing capital value/yield - movements. Irrelevant if held to term.  Only relevant if bond is to be sold.

We probably also agree that

Redemption value - return of principal - is not variable. The nominal value of the bond.  Is known at purchase*.

*Strictly - you won't know the values of inflation for index linkers but you will know that you will be getting it.

Now I accept this subtlety may be included in what was intended implied or treated as assumed knowledge
Of the quote.  That's all I disagree about.

Or maybe I don't understand how they work and this is all rubbish in which case I am sorry for misleading OP and confusing them further

I think that covers most possibilities

OldScientist

gm0's explanation is correct for the nominal gilts currently in issue, the redemption price will be £100.

The issue price will depend on several things. a) They are sold by auction so the price will be determined by what the larger buyers (e.g., pensions) are willing to pay for UK debt (which, presumably, will give yields that won't be too far from any existing gilts of similar coupon and maturity), and b) the coupon, my understanding is this is set to the nearest 0.125% of current market yields such that the issue price is likely to be slightly below par.

Just for interest here are the price histories of two gilts. The first, where the gilt was issued in 1966 and the price spent most of the time below par and the second where the gilt was issued in 2007 the price spent most of the time between issue and redemption above par (prices obtained from the database published by Ellison and Scott, 2020). Note that the first price plotted in each graph is a few days/weeks after issue and therefore is not the actual issue/auction price.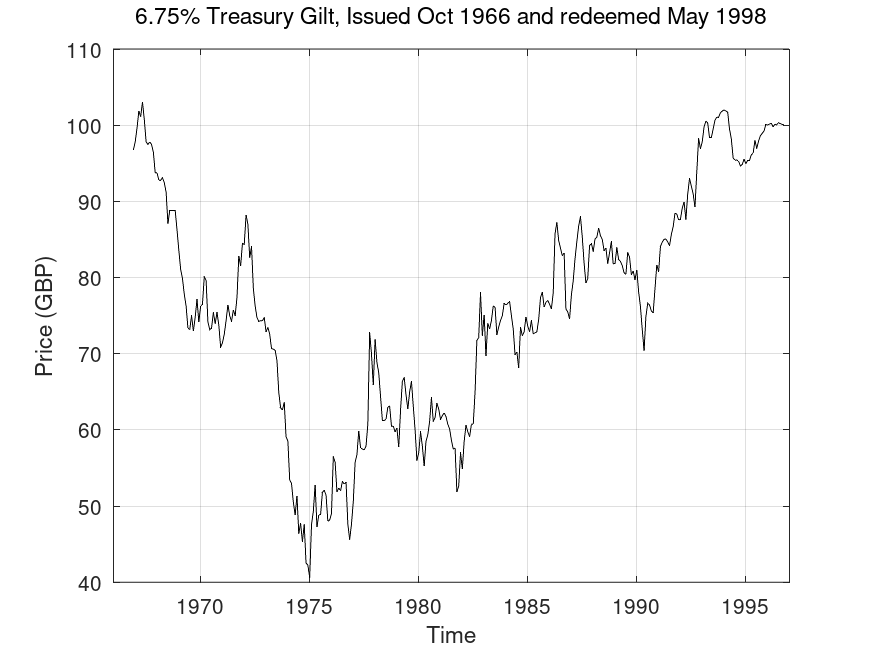



Here the investor would have seen the capital value of their gilt drop by 60% over the first decade or so and this would also have been coupled with high inflation in the 1970s (the purchasing power of the £100 in 1998 was about 1/8th of that in 1966). However, for someone using such a gilt to provide retirement income, the 6.75% coupon was not too bad. It is also worth noting that the variation in price over the last 5 years or so was relatively small.




Here, the investor could have sold the gilt at almost any time before maturity and made a capital gain (although would then have had to decide what they would replace it with). The price steadily approached par over the last 4 years or so before redemption. Holding the gilt would have allowed a retirement income of 5% (rather nice when interest rates were low in 2016 or so).

The two cases nicely illustrate that almost anything can happen between issue and redemption.

So, in the absence of government default, the certainties of investing in individual gilts are
1) Half the coupon will be paid every six months (i.e. for the 5% gilt illustrated above, the holder of £100 worth of that gilt would have received £2.50 in March and September of each year).
2) The par value of £100 will be returned on the redemption date.

One of the uncertainties for both individual gilts is the price before the redemption date is unknowable in advance. For bond funds, the price is wholly dependent on market yields.

wmb194

The results have finally been announced, see below. Looks like the bidders were lucky gilts weakened on the day of the auction; they paid £99.441 for a YTM of 4.085%.

https://www.dmo.gov.uk/data/pdfdatareport?reportCode=D2.1PROF7

gabiieve

OldScientist said:

gm0's explanation is correct for the nominal gilts currently in issue, the redemption price will be £100.

The issue price will depend on several things. a) They are sold by auction so the price will be determined by what the larger buyers (e.g., pensions) are willing to pay for UK debt (which, presumably, will give yields that won't be too far from any existing gilts of similar coupon and maturity), and b) the coupon, my understanding is this is set to the nearest 0.125% of current market yields such that the issue price is likely to be slightly below par.

Just for interest here are the price histories of two gilts. The first, where the gilt was issued in 1966 and the price spent most of the time below par and the second where the gilt was issued in 2007 the price spent most of the time between issue and redemption above par (prices obtained from the database published by Ellison and Scott, 2020). Note that the first price plotted in each graph is a few days/weeks after issue and therefore is not the actual issue/auction price.



Here the investor would have seen the capital value of their gilt drop by 60% over the first decade or so and this would also have been coupled with high inflation in the 1970s (the purchasing power of the £100 in 1998 was about 1/8th of that in 1966). However, for someone using such a gilt to provide retirement income, the 6.75% coupon was not too bad. It is also worth noting that the variation in price over the last 5 years or so was relatively small.




Here, the investor could have sold the gilt at almost any time before maturity and made a capital gain (although would then have had to decide what they would replace it with). The price steadily approached par over the last 4 years or so before redemption. Holding the gilt would have allowed a retirement income of 5% (rather nice when interest rates were low in 2016 or so).

The two cases nicely illustrate that almost anything can happen between issue and redemption.

So, in the absence of government default, the certainties of investing in individual gilts are
1) Half the coupon will be paid every six months (i.e. for the 5% gilt illustrated above, the holder of £100 worth of that gilt would have received £2.50 in March and September of each year).
2) The par value of £100 will be returned on the redemption date.

One of the uncertainties for both individual gilts is the price before the redemption date is unknowable in advance. For bond funds, the price is wholly dependent on market yields.

This is a great post. Thank you for sharing these images, they gave me some clarity on gilts.

I have a question: if interest rates on bank accounts were to stay above 4.085% (plus the difference between £100 and £99.441) until 2031, would money in a savings account outperform these gilts or have I missed something?

Andreg

The 0.45%% annual management charge from HL seems very high.  HSBC Investdirect only charge £10.50 per quarter flat fee (although they charge a higher £40 dealing fee), and I believe Fidelity also probably offer better value.

zagfles

Andreg said:

The 0.45%% annual management charge from HL seems very high.  HSBC Investdirect only charge £10.50 per quarter flat fee (although they charge a higher £40 dealing fee), and I believe Fidelity also probably offer better value.

HL charge zero annual management charge to hold gilts unwrapped. 
In an ISA it's 0.45% capped at £45 a year, and in a SIPP capped at £200. 

coyrls

gabiieve said:

OldScientist said:

gm0's explanation is correct for the nominal gilts currently in issue, the redemption price will be £100.

The issue price will depend on several things. a) They are sold by auction so the price will be determined by what the larger buyers (e.g., pensions) are willing to pay for UK debt (which, presumably, will give yields that won't be too far from any existing gilts of similar coupon and maturity), and b) the coupon, my understanding is this is set to the nearest 0.125% of current market yields such that the issue price is likely to be slightly below par.

Just for interest here are the price histories of two gilts. The first, where the gilt was issued in 1966 and the price spent most of the time below par and the second where the gilt was issued in 2007 the price spent most of the time between issue and redemption above par (prices obtained from the database published by Ellison and Scott, 2020). Note that the first price plotted in each graph is a few days/weeks after issue and therefore is not the actual issue/auction price.



Here the investor would have seen the capital value of their gilt drop by 60% over the first decade or so and this would also have been coupled with high inflation in the 1970s (the purchasing power of the £100 in 1998 was about 1/8th of that in 1966). However, for someone using such a gilt to provide retirement income, the 6.75% coupon was not too bad. It is also worth noting that the variation in price over the last 5 years or so was relatively small.




Here, the investor could have sold the gilt at almost any time before maturity and made a capital gain (although would then have had to decide what they would replace it with). The price steadily approached par over the last 4 years or so before redemption. Holding the gilt would have allowed a retirement income of 5% (rather nice when interest rates were low in 2016 or so).

The two cases nicely illustrate that almost anything can happen between issue and redemption.

So, in the absence of government default, the certainties of investing in individual gilts are
1) Half the coupon will be paid every six months (i.e. for the 5% gilt illustrated above, the holder of £100 worth of that gilt would have received £2.50 in March and September of each year).
2) The par value of £100 will be returned on the redemption date.

One of the uncertainties for both individual gilts is the price before the redemption date is unknowable in advance. For bond funds, the price is wholly dependent on market yields.

This is a great post. Thank you for sharing these images, they gave me some clarity on gilts.

I have a question: if interest rates on bank accounts were to stay above 4.085% (plus the difference between £100 and £99.441) until 2031, would money in a savings account outperform these gilts or have I missed something?

The 4.085% includes the difference between £100 and £99.441.  You would need to compare it with a seven year fixed rate account with interest paid every 6 months but as such a product doesn't exist you could compare it to a 5 year fixed rate account with interest paid annually.  You can't compare to bank account interest as that could change many times over a seven year period.

OldScientist

gabiieve said:

OldScientist said:

gm0's explanation is correct for the nominal gilts currently in issue, the redemption price will be £100.

The issue price will depend on several things. a) They are sold by auction so the price will be determined by what the larger buyers (e.g., pensions) are willing to pay for UK debt (which, presumably, will give yields that won't be too far from any existing gilts of similar coupon and maturity), and b) the coupon, my understanding is this is set to the nearest 0.125% of current market yields such that the issue price is likely to be slightly below par.

Just for interest here are the price histories of two gilts. The first, where the gilt was issued in 1966 and the price spent most of the time below par and the second where the gilt was issued in 2007 the price spent most of the time between issue and redemption above par (prices obtained from the database published by Ellison and Scott, 2020). Note that the first price plotted in each graph is a few days/weeks after issue and therefore is not the actual issue/auction price.



Here the investor would have seen the capital value of their gilt drop by 60% over the first decade or so and this would also have been coupled with high inflation in the 1970s (the purchasing power of the £100 in 1998 was about 1/8th of that in 1966). However, for someone using such a gilt to provide retirement income, the 6.75% coupon was not too bad. It is also worth noting that the variation in price over the last 5 years or so was relatively small.




Here, the investor could have sold the gilt at almost any time before maturity and made a capital gain (although would then have had to decide what they would replace it with). The price steadily approached par over the last 4 years or so before redemption. Holding the gilt would have allowed a retirement income of 5% (rather nice when interest rates were low in 2016 or so).

The two cases nicely illustrate that almost anything can happen between issue and redemption.

So, in the absence of government default, the certainties of investing in individual gilts are
1) Half the coupon will be paid every six months (i.e. for the 5% gilt illustrated above, the holder of £100 worth of that gilt would have received £2.50 in March and September of each year).
2) The par value of £100 will be returned on the redemption date.

One of the uncertainties for both individual gilts is the price before the redemption date is unknowable in advance. For bond funds, the price is wholly dependent on market yields.

This is a great post. Thank you for sharing these images, they gave me some clarity on gilts.

I have a question: if interest rates on bank accounts were to stay above 4.085% (plus the difference between £100 and £99.441) until 2031, would money in a savings account outperform these gilts or have I missed something?

The short answer, is yes - if the interest rates remain above the yield to maturity of about 4.1% (there are some wrinkles with this, but for a hypothetical question this is accurate enough), then holding the money in a bank account would do better. If the interest rates were to be below this, then the opposite would be true. The problem is that it is not possible to know beforehand since we have no idea what interest rates will do (the one thing I am fairly certain about is that they will not be constant!).

GeoffTF

coyrls said:

You would need to compare it with a seven year fixed rate account with interest paid every 6 months but as such a product doesn't exist you could compare it to a 5 year fixed rate account with interest paid annually.  You can't compare to bank account interest as that could change many times over a seven year period.

Here is a list of 7 year fixed rate accounts:

https://www.fairerfinance.com/ratings/product-ratings/7-year-fixed-rate-accounts

newatc

Am I right in thinking that in purchasing Gilts on HL and holding in Share Account the costs would be 
Dealing Charges of £11.95 on entry and exit
No charges for Holding
Stamp Duty?

Additionally interest paid out would be subject to  tax.